Matematiikka
Oppiaineen tehtävä
Matematiikan opetuksen tehtävänä on kehittää oppilaiden loogista, täsmällistä ja luovaa matemaattista ajattelua. Opetus luo pohjan matemaattisten käsitteiden ja rakenteiden ymmärtämiselle sekä kehittää oppilaiden kykyä käsitellä tietoa ja ratkaista ongelmia. Matematiikan kumulatiivisesta luonteesta johtuen opetus etenee systemaattisesti. Konkretia ja toiminnallisuus ovat keskeinen osa matematiikan opetusta ja opiskelua. Oppimista tuetaan hyödyntämällä tieto- ja viestintäteknologiaa.
Matematiikan opetus tukee oppilaiden myönteistä asennetta matematiikkaa kohtaan sekä positiivista minäkuvaa matematiikan oppijoina. Se kehittää myös viestintä-, vuorovaikutus- ja yhteistyötaitoja. Matematiikan opiskelu on tavoitteellista ja pitkäjänteistä toimintaa, jossa oppilaat ottavat vastuuta omasta oppimisestaan.
Opetus ohjaa oppilaita ymmärtämään matematiikan hyödyllisyyden omassa elämässään ja laajemmin yhteiskunnassa. Opetus kehittää oppilaiden kykyä käyttää ja soveltaa matematiikkaa monipuolisesti.
Vuosiluokat 1-2
Oppiaineen tehtävä
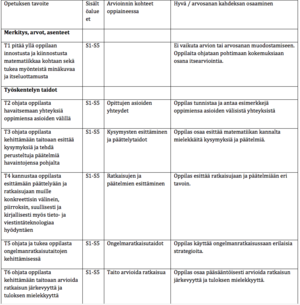
Vuosiluokkien 1−2 matematiikan opetuksessa oppilaille tarjotaan monipuolisia kokemuksia matemaattisten käsitteiden ja rakenteiden muodostumisen perustaksi. Opetuksessa hyödynnetään eri aisteja. Opetus kehittää oppilaiden kykyä ilmaista matemaattista ajatteluaan konkreettisin välinein, suullisesti, kirjallisesti ja piirtäen sekä tulkiten kuvia. Matematiikan opetus luo vahvan pohjan lukukäsitteen ja kymmenjärjestelmän ymmärtämiseksi sekä laskutaidolle.
Oppimisympäristöihin ja työtapoihin liittyvät tavoitteet
Opetuksen lähtökohtana käytetään oppilaille tuttuja ja kiinnostavia aiheita ja ongelmia. Tavoitteena on luoda oppimisympäristö, jossa matematiikkaa opiskellaan toiminnallisesti ja välineiden avulla. Opetuksessa käytetään vaihtelevia työtapoja. Oppilaat tottuvat työskentelemään sekä itsenäisesti että yhdessä. Pedagogisesti ohjatut leikit ja pelit ovat yksi tärkeä työtapa. Opetuksessa ja opiskelussa käytetään tieto- ja viestintäteknologiaa.
Ohjaus, eriyttäminen ja tuki
Koulun alkaessa selvitetään, mitä oppilaat jo osaavat ja millaisia eroja osaamisessa on. Kumulatiivisena oppiaineena matematiikan perusasioiden hallinta on välttämätön edellytys uusien sisältöjen oppimiselle. Oppilaille tarjotaan tukea puutteellisten, aiemmin opittujen tietojen ja taitojen täydentämiseen sekä uusien sisältöjen oppimiseen. Matematiikan oppimisen valmiuksien kehittämiselle ja matematiikan oppimiselle varataan riittävästi aikaa ja tuetaan oppimista systemaattisesti. Oppilaiden matematiikan osaamista ja taitojen kehittymistä seurataan jatkuvasti. Tarjottava tuki antaa oppilaille mahdollisuuden kehittää taitojaan niin, että oppimisen ja osaamisen ilo säilyvät. Oppilaille tarjotaan sopivia välineitä oppimisen tueksi ja luodaan mahdollisuuksia oivaltaa ja ymmärtää itse. Oppilaille turvataan mahdollisuus riittävään harjoitteluun.
Taitaville oppilaille tarjotaan mahdollisuus syventää vuosiluokkien 1-2 sisältöjen ymmärtämistä. Sisältöalueita voivat olla esimerkiksi luonnollisten lukujen ominaisuudet, erilaiset lukujonot, geometria, luova ongelmanratkaisu ja vaativammat peruslaskutoimitusten sovellukset.
Oppilaan oppimisen arviointi
Vuosiluokilla 1-2 oppimisen arvioinnin päätehtävänä lukuvuoden aikana on tukea ja edistää oppilaiden matemaattisen ajattelun ja osaamisen kehittymistä kaikilla tavoitealueilla. Matematiikan oppimisen arviointi ja palaute on kannustavaa. Oppilaita rohkaistaan vahvuuksien ylläpitämiseen ja kehittymässä olevien taitojen harjoittelemiseen. Oppilaita ohjataan huomaamaan oman oppimisensa eteneminen.
Oppilaiden matematiikan ymmärtämisen ja osaamisen tasoa voidaan selvittää puheen, välineiden, piirtämisen tai kirjallisen työskentelyn avulla. Oppilailla tulee olla mahdollisuus osoittaa edistymistään eri tavoin. On tärkeää arvioida ratkaisujen oikeellisuuden lisäksi tekemisen tapaa ja sujuvuutta.
Oppimisprosessin kannalta keskeisiä arvioinnin ja palautteen antamisen kohteita matematiikassa ovat
- edistyminen lukukäsitteen ymmärtämisessä ja lukujonotaidoissa
- edistyminen kymmenjärjestelmän ymmärtämisessä
- edistyminen laskutaidon sujuvuudessa
- edistyminen kappaleiden ja kuvioiden luokittelun taidoissa
- edistyminen matematiikan käyttämisessä ongelmanratkaisussa.
Laaja-alainen osaaminen
Ajattelu ja oppimaan oppiminen
- toteutuu sitomalla matematiikka oppilaan arkipäivän tilanteisiin
Kulttuurinen osaaminen, vuorovaikutus ja ilmaisu
- esittää päätelmiään eri tavoin
Itsestä huolehtiminen ja arjen taidot
- itseluottamuksen, myönteisen minäkuvan ja käsityksen itsestään osaajana kehittäminen
Monilukutaito
- numeroiden lukeminen, kuvaajien lukeminen, lukukäsitteen ymmärtäminen, geometriset käsitteet
TVT-osaaminen
- yksinkertaiset vaiheittaiset toimintaohjeet ja niiden laatiminen ja noudattaminen (leikit, pelit), tietoteknisten sovellusten käyttö harjoitteluvälineenä
Työelämätaidot ja yrittäjyys
- vastuu omasta työstä, ongelmanratkaisutaidot
Vuosiluokka 1
Tavoitteet
- Oppilas innostuu ja kiinnostuu matematiikasta monipuolisesti. Samalla oppilas saa myönteisen minäkuvan matematiikan oppijana (T1).
- Oppilas tutkii lukujen ominaisuuksia (T4, T5, T6, T7).
- Oppilas harjoittelee peruslaskutoimituksia ja päässälaskustrategioita. Oppilas avaa ajatuksiaan kertomalla, piirtäen, kirjoittamalla ja tieto- ja viestintäteknologiaa hyödyntäen (T3,T4, T8).
- Geometriassa oppilas harjoittelee mittaamista, kuvioiden luokittelua sekä tutustuu kappaleiden ominaisuuksiin ja rakentaa erilaisia kappaleita (T2, T4, T9, T10).
- Oppilas käsittelee ja tulkitsee tilastoja omassa lähiympäristössään (T2,T4, T11).
- Oppilas tutustuu ohjelmoinnin ideaan pelien ja leikkien yhteydessä keksimällä yksinkertaisia toimintaohjeita ja noudattaa niitä (T12).
Sisällöt
tutustutaan:
- kymmenenylityksen harjoittelu
- päässälaskustrategiat
- mittaamisen perusteet (yksiköt: m, cm, kg, g, l, dl, h ja min)
- ohjelmoinnin idea
- lukujono
varmennetaan:
- lukualue 0-20 yhteen- ja vähennyslasku
- lukukäsite (lukumäärä, suuruusvertailu, numeromerkit, hajotelmat 1-10, parillisuus)
- yksinkertaisten tasokuvioiden havainnoiminen, tunnistaminen, ominaisuuksien nimeäminen sekä luokittelu (ympyrä, nelikulmio ja kolmio)
Vuosiluokka 2
Tavoitteet
- Oppilas innostuu ja kiinnostuu matematiikasta monipuolisesti. Samalla oppilas saa myönteisen minäkuvan matematiikan oppijana (T1).
- Oppilas tutkii lukujen ominaisuuksia (T4, T5, T6, T7).
- Oppilas harjoittelee peruslaskutoimituksia ja päässälaskustrategioita. Oppilas avaa ajatuksiaan kertomalla, piirtäen, kirjoittamalla ja tieto- ja viestintäteknologiaa hyödyntäen. (T3,T4, T8)
- Geometriassa oppilas harjoittelee mittaamista, kuvioiden luokittelua sekä tutustuu kappaleiden ominaisuuksiin ja rakentaa erilaisia kappaleita (T2, T4, T9, T10).
- Oppilas käsittelee ja tulkitsee tilastoja omassa lähiympäristössään (T2,T4, T11).
- Oppilas tutustuu ohjelmoinnin ideaan pelien ja leikkien yhteydessä keksimällä yksinkertaisia toimintaohjeita ja noudattaa niitä (T12).
Sisällöt
tutustutaan:
- lukukäsite (kertolaskun käsite, monikerrat ja puolittaminen, kerto- ja jakolaskun yhteys)
- yksinkertaisten kappaleiden havainnoiminen, tunnistaminen, ominaisuuksien nimeäminen, luokittelu ja rakentelu
varmennetaan:
- lukujono
- lukualue 0-100
- kymmenenylitys
- kertotaulut 1-5 ja 10
- yksinkertaisten tasokuvioiden havainnoiminen, tunnistaminen, ominaisuuksien nimeäminen, luokittelu ja rakentelu (ympyrä ja nelikulmio)
- ohjelmoinnin idea
syvennetään:
- yhteen- ja vähennyslaskua
- mittaamista mittayksiköillä (m, cm, kg, g, l, dl, h ja min)
Vuosiluokat 3-6
Oppiaineen tehtävä
Vuosiluokkien 3−6 matematiikan opetuksessa tarjotaan kokemuksia, joita oppilaat hyödyntävät matemaattisten käsitteiden ja rakenteiden muodostamisessa. Opetus kehittää oppilaiden taitoja esittää matemaattista ajatteluaan ja ratkaisujaan eri tavoilla ja välineillä. Monipuolisten ongelmien ratkaisu yksin ja ryhmässä sekä erilaisten ratkaisutapojen vertailu ovat opetuksessa keskeistä. Matematiikan opetuksessa varmennetaan ja laajennetaan oppilaiden lukukäsitteen ja kymmenjärjestelmän ymmärtämistä. Lisäksi kehitetään laskutaidon sujuvuutta.
Oppimisympäristöihin ja työtapoihin liittyvät tavoitteet
Opetuksen lähtökohtana käytetään oppilaille tuttuja ja kiinnostavia aiheita ja ongelmia. Matematiikkaa opiskellaan edelleen oppimisympäristössä, jossa konkretisointi ja välineet ovat keskeisessä asemassa. Välineet tulee olla helposti saatavilla. Opetuksessa käytetään vaihtelevia työtapoja. Oppilailla on mahdollisuus vaikuttaa työtapojen valintaan. Työskennellään sekä yhdessä että itsenäisesti. Oppimispelit ja -leikit ovat yksi tärkeä ja oppilaita motivoiva työtapa. Tieto- ja viestintäteknologiaa sekä laskinta hyödynnetään opetuksessa ja opiskelussa.
Konkreettiset oppimisvälineet säilyvät aktiivisessa käytössä. Oppimisympäristöä laajennetaan oppilaan ikätason mukaisesti ja annetaan mahdollisuus vaikuttaa työtapojen valintaan.
Oppilaalle tarjotaan edelleen erilaisia välineitä esim. värisauvoja, luonnonmateriaaleja, kymmenjärjestelmävälineitä, palikoita, murtokakkuja, laskukiekkoja, noppia, geometrisia malleja ja mittavälineitä. Välineet voivat olla myös oppilaiden itse tuottamia. Oppimisympäristönä hyödynnetään myös lähiympäristöä. Harjoittelussa käytetään apuna tieto- ja viestintätekniikkaa sekä laskinta.
Ohjaus, eriyttäminen ja tuki
Jokaisella oppilaalla on mahdollisuus saada opetusta myös aiempien vuosiluokkien keskeisimmistä sisällöistä, jos hän ei hallitse niitä riittävästi. Lisäksi annetaan ennakoivaa tukea uusien sisältöjen oppimiseksi. Matematiikan oppimiselle on varattava riittävästi aikaa ja tuen on oltava systemaattista. Oppilaiden matematiikan osaamista ja taitojen kehittymistä seurataan jatkuvasti. Tarjottava tuki antaa oppilaille mahdollisuuden kehittää taitojaan niin, että myönteinen asenne ja kyvykkyyden tunne vahvistuvat. Oppilaille tarjotaan sopivia välineitä oppimisen tueksi ja heille tarjotaan mahdollisuuksia oivaltaa ja ymmärtää itse. Jokaiselle oppilaalle turvataan mahdollisuus riittävään harjoitteluun.
Taitavia oppilaita tuetaan tarjoamalla heille vaihtoehtoisia työskentelymuotoja ja rikastuttamalla käsiteltäviä sisältöjä. Sisältöalueita voivat olla esimerkiksi lukujen ominaisuudet, erilaiset lukujonot, geometria, luova ongelmanratkaisu ja matematiikan sovellukset.
Oppilaalle tarjotaan mahdollisuus käyttää konkreettisia apuvälineitä. Laskinta käytetään tarpeen mukaan eriyttämisen välineenä. Oppilaalle tarjotaan mahdollisuus saada opetusta edellisten vuosiluokkien sisällöistä. Vuosiluokkakokonaisuuden (3-6) sisällä sisältöjä voidaan laajentaa. Oppilaalle tarjotaan oman tasonsa mukaisia tehtäviä ja haasteita.
Oppilaan oppimisen arviointi
Vuosiluokilla 3-6 oppimisen arvioinnin päätehtävänä lukuvuoden aikana on tukea ja edistää oppilaiden matemaattisen ajattelun ja osaamisen kehittymistä kaikilla tavoitealueilla. Arviointi on monipuolista ja palaute ohjaavaa ja rakentavaa. Ne tukevat oppilaiden matemaattisten taitojen kehittymistä ja rohkaisevat tarvittaessa uuteen yrittämiseen. Oppilaita ohjataan arvioimaan omaa oppimistaan ja tiedostamaan vahvuuksiaan. Palaute auttaa oppilaita ymmärtämään, mitä tietoja ja taitoja tulisi edelleen kehittää ja miten. Lisäksi oppilaita ohjataan kiinnittämään huomiota tapaansa työskennellä sekä tiedostamaan asennettaan matematiikan opiskelua kohtaan.
Oppilailta edellytetään aiempaa enemmän matemaattisen ajattelunsa esilletuomista puheen, välineiden, piirtämisen ja kirjallisen työskentelyn avulla. Arvioinnin kohteena ovat tekemisen tapa, ratkaisujen oikeellisuus sekä taito soveltaa opittua.
Yhdessä työskenneltäessä arvioidaan sekä ryhmän jäsenten että koko ryhmän toimintaa ja tuotosta. Palautteella ohjataan oppilaita ymmärtämään jokaisen ryhmän jäsenen työskentelyn ja kehittymisen merkitys. Oppilaita ohjataan tuotosten ja toiminnan arvioimiseen.
TAULUKKO ARVIOINTIKRITEEREISTÄ 6. VUOSILUOKAN PÄÄTYTTYÄ
Laaja-alainen osaaminen
Ajattelu ja oppimaan oppiminen
- toteutuu sitomalla matematiikka oppilaan arkipäivän tilanteisiin
Kulttuurinen osaaminen, vuorovaikutus ja ilmaisu
- esittää päätelmiään eri tavoin
Itsestä huolehtiminen ja arjen taidot
- itseluottamuksen, myönteisen minäkuvan ja käsityksen itsestään osaajana kehittäminen
Monilukutaito
- numeroiden lukeminen, kuvaajien lukeminen, lukukäsitteen ymmärtäminen, geometriset käsitteet
TVT-osaaminen
- vaiheittaiset toimintaohjeet ja niiden laatiminen ja noudattaminen (leikit, pelit), tietoteknisten sovellusten käyttö harjoitteluvälineenä
Työelämätaidot ja yrittäjyys
- vastuu omasta työstä, ongelmanratkaisutaidot
Vuosiluokka 3
Tavoitteet
OPETUKSEN YHTEISET VALTAKUNNALLISET TAVOITTEET T1-T14
- Opetuksen tavoitteena on pitää yllä oppilaan innostusta ja kiinnostusta matematiikkaa kohtaan sekä tukea myönteistä minäkuvaa ja itseluottamusta.
- Oppilas tutustuu murto- ja desimaalilukujen käsitteisiin sekä sisältö- ja ositusjakoon konkreettisin apuvälinein arkielämän tilanteiden kautta.
- Oppilas tutustuu geometrian peruskäsitteisiin, koordinaatiston ensimmäiseen neljännekseen sekä graafisen ohjelmoinnin alkeisiin hyödyntäen tietotekniikkaa mahdollisuuksien mukaan.
- Oppilas tutkii edelleen erilaisia lukujonoja ja huomaa säännönmukaisuuksia.
- Oppilas osaa kertotaulut 1-10.
- Oppilas harjoittelee edelleen peruslaskutoimituksia päässä sekä yhteen-ja vähennyslaskuja allekkain.
Sisällöt
tutustutaan:
- murtoluvun käsite
- desimaaliluvut
- sisältö- ja ositusjako
- kertolaskut allekkain
- geometrian peruskäsitteet: piste, jana, suora
- koordinaatisto 1. neljännes graafisen ohjelmoinnin alkeet
varmennetaan:
- lukujono
- yhteen- ja vähennyslasku allekkain
- kertolaskun käsite
- kertotaulut (1-10)
syvennetään:
- 10-järjestelmä
- peruslaskutoimitukset luonnollisilla luvuilla
Vuosiluokka 4
Tavoitteet
OPETUKSEN YHTEISET VALTAKUNNALLISET TAVOITTEET T1-T14
- Opetuksen tavoitteena on pitää yllä oppilaan innostusta ja kiinnostusta matematiikkaa kohtaan sekä tukea myönteistä minäkuvaa ja itseluottamusta.
- Oppilas harjoittelee pyöristämistä, lukuyksiköittäin jakamista ja graafisen ohjelmoinnin perusteita.
- Oppilas osaa desimaalilukujen yksinkertaisia laskutoimituksia ja murtolukujen yhteen- ja vähennyslaskun.
- Geometriassa oppilas perehtyy tasokuvioiden pinta-alaan ja piiriin sekä harjoittelee mittayksiköiden muunnoksia sekä kulmien piirtämistä, mittaamista ja luokittelua.
Sisällöt
tutustutaan:
- pyöristäminen
- lukuyksiköittäin jakaminen
- graafisen ohjelmoinnin perusteet
varmennetaan:
- kertolasku allekkain
- desimaaliluvut (yksinkertaiset laskutoimitukset)
- murtoluvut (yhteen- ja vähennyslasku)
- kulmat (piirtäminen, mittaaminen, luokittelu)
- tasokuviot (kolmio, nelikulmio, ympyrä)
- pinta-ala ja piiri (kolmio ja nelikulmio)
- mittayksiköiden muunnokset (pituus ja pinta-ala)
syvennetään:
- peruslaskutoimitukset
Vuosiluokka 5
Tavoitteet
OPETUKSEN YHTEISET VALTAKUNNALLISET TAVOITTEET T1-T14
- Opetuksen tavoitteena on pitää yllä oppilaan innostusta ja kiinnostusta matematiikkaa kohtaan sekä tukea myönteistä minäkuvaa ja itseluottamusta.
- Oppilas harjoittelee prosenttilaskentaa sekä ymmärtää sen yhteyden murto- ja desimaalilukuihin sekä prosentin käsitteeseen.
- Oppilas tutustuu negatiivisiin kokonaislukuihin.
- Oppilas havaitsee erilaisia symmetrioita esimerkiksi taiteen avulla.
- Oppilas osaa käyttää mittakaavaa arkielämän tilanteissa esim. kartat ja suurennokset.
- Oppilas harjoittelee murtolukujen laskutoimituksia.
- Oppilas harjoittelee koko koordinaatiston käyttöä.
- Oppilas oppii mittaamaan ja laskemaan suorakulmaisen särmiön tilavuuden sekä osaa luokitella muitakin geometrisia kappaleita.
- Oppilas hallitsee jo opitut peruslaskutoimitukset ja osaa soveltaa niitä arkielämän tilanteissa.
Sisällöt
tutustutaan:
- prosenttilaskenta (yhteys murto- ja desimaalilukuihin, prosentin käsite) kokonaisluvut
- symmetria suoran suhteen (kierto- ja siirtosymmetriat)
- mittakaava (esim. suurennokset, pienennökset ja kartan käyttö).
varmennetaan:
- murtolukujen yhteen- ja vähennyslaskut
- murtolukujen kertominen ja jakaminen luonnollisella luvulla
- koordinaatisto (kaikki neljännekset)
- suorakulmainen särmiö (yksikönmuunnokset, tilavuus mittaamalla ja laskemalla)
- geometristen kappaleiden luokittelu (lieriö ja kartio)
syvennetään:
- peruslaskutoimitukset laajentuneella lukualueella
Vuosiluokka 6
Tavoitteet
OPETUKSEN YHTEISET VALTAKUNNALLISET TAVOITTEET T1-T14
- Opetuksen tavoitteena on pitää yllä oppilaan innostusta ja kiinnostusta matematiikkaa kohtaan sekä tukea myönteistä minäkuvaa ja itseluottamusta (T1).
- Oppilas oppii ratkaisemaan yhtälöitä päättelemällä.
- Oppilas oppii piirtämään kuvaajia ja tulkitsemaan tilastoja taulukkolaskentaohjelman avulla.
- Oppilas harjoittelee edelleen toimimista kokonaislukualueella.
- Oppilas harjoittelee prosenttilaskuja.
- Oppilas osaa päätellä helppoja todennäköisyyksiä.
- Oppilas osaa ohjelmoida ohjelman graafisessa ohjelmointiympäristössä.
- Oppilas varmentaa edellisten vuosiluokkien keskeisiä sisältöjä peruslaskutoimituksista, mittayksiköiden muunnoksista ja pyöristämisestä.
Sisällöt
tutustutaan:
- yhtälö (ratkaiseminen päättelemällä)
- taulukkolaskentaohjelma
varmennetaan:
- negatiivisen kokonaisluvun käsite
- prosenttilaskut
- todennäköisyys
- tilastot (tulkinta ja piirtäminen)
- tilastolliset tunnusluvut (moodi, keskiarvo, suurin ja pienin arvo)
- graafinen ohjelmointi
syvennetään:
- mittayksiköiden muunnokset (pituus, pinta-ala, tilavuus, massa, aika)
- peruslaskutoimitukset rationaaliluvuilla
Vuosiluokat 7-9
Oppiaineen tehtävä
Vuosiluokkien 7−9 matematiikan opetuksen tehtävänä on vahvistaa matemaattista yleissivistystä. Opetuksessa syvennetään matemaattisten käsitteiden ja niiden välisten yhteyksien ymmärtämistä. Opetus innostaa oppilaita löytämään ja hyödyntämään matematiikkaa omassa elämässään. Oppilaiden valmiuksiin kuuluvat ongelmien matemaattinen mallintaminen ja ratkaiseminen. Matematiikan opetus ohjaa oppilaita tavoitteelliseen, täsmälliseen, keskittyneeseen ja pitkäjänteiseen toimintaan. Oppilaita rohkaistaan esittämään ratkaisujaan ja keskustelemaan niistä. Opetuksessa kehitetään oppilaiden yhteistyötaitoja.
Oppimisympäristöihin ja työtapoihin liittyvät tavoitteet
Opetuksen lähtökohdat valitaan oppilaita kiinnostavista aiheista, ilmiöistä ja niihin liittyvistä ongelmista. Konkretia toimii edelleen tärkeänä osana matematiikan opiskelua. Rohkaistaan oppilaita käyttämään ajattelua tukevia piirroksia ja välineitä. Opetuksessa käytetään vaihtelevia työtapoja. Ongelmia matematisoidaan, ratkaistaan ja tulkitaan yksin ja yhdessä. Yhdessä työskennellessä jokainen toimii sekä itsensä että ryhmän hyväksi. Oppimispelit ovat yksi motivoiva työtapa. Tieto- ja viestintäteknologiaa, kuten taulukkolaskentaa ja dynaamista geometriaohjelmistoa, hyödynnetään opetuksen, oppimisen, tuottamisen, arvioinnin sekä luovuuden välineenä.
Konkreettiset oppimisvälineet säilyvät edelleen aktiivisessa käytössä. Oppimisympäristöä laajennetaan oppilaan ikätason mukaisesti ja oppilaalla on mahdollisuus vaikuttaa työtapojen valintaan.
Oppilaalle tarjotaan edelleen erilaisia välineitä esim. värisauvoja, geolauta, kymmenjärjestelmävälineet, palikoita, murtokakkuja, loogisia paloja, laskukiekkoja, noppia, geometrisia malleja ja mittavälineitä. Oppimisympäristönä hyödynnetään myös lähiympäristöä ja yhteistyökumppaneita. Harjoittelussa käytetään apuna tieto- ja viestintätekniikkaa. Harjoittelua pyritään edistämään sopivilla dynaamisilla geometriaohjelmistoilla. Tutustutaan uusiin ohjelmointiympäristöihin, jotka sopivat matematiikan sisältöjen harjoitteluun ja jatketaan graafisten ohjelmointiympäristöjen käyttöä.
Ohjaus, eriyttäminen ja tuki
Jokaisella oppilaalla tulee olla mahdollisuus saada opetusta myös aiempien vuosiluokkien keskeisimmistä sisällöistä, jos hän ei hallitse niitä riittävästi. Lisäksi annetaan ennakoivaa tukea tarvittaessa uusien sisältöjen oppimiseksi. Oppilaiden matematiikan osaamista ja taitojen kehittymistä seurataan jatkuvasti yhdessä oppilaiden kanssa. Oppilaille korostetaan asioiden ymmärtämisen tärkeyttä. Oppilaita tuetaan suurempien asiakokonaisuuksien hahmottamisessa ja yhteyksien löytämisessä. Eriyttämisessä otetaan huomioon jokaisen oppilaan osaaminen ja annetaan mahdollisuus onnistumisen elämyksiin.
Sisältöjä voidaan rikastuttaa syventämällä yhteisesti käsiteltävää aihetta oppilaiden kiinnostuksen ja taitotason mukaan. Taitavia oppilaita tuetaan tarjoamalla heille vaihtoehtoisia työskentelymuotoja, kuten esimerkiksi erilaisia projekteja ja ongelmalähtöisiä tutkimustehtäviä oppilaita kiinnostavista matemaattisista aiheista.
Oppilaalla on mahdollisuus käyttää konkreettisia apuvälineitä niin halutessaan. Oppilaalle tarjotaan mahdollisuus saada opetusta edellisten vuosiluokkien sisällöistä. Vuosiluokkakokonaisuuden (7-9) sisällä sisältöjä voidaan laajentaa. Oppilaalle tarjotaan oman tasonsa mukaisia tehtäviä ja haasteita.
Oppilaan oppimisen arviointi
Monipuolisella arvioinnilla ja kannustavalla palautteella tuetaan matemaattisen ajattelun ja itseluottamuksen kehittymistä ja ylläpidetään ja vahvistetaan opiskelumotivaatiota. Palaute tukee oppilaiden myönteistä minäkuvaa matematiikan oppijana. Oppilaille annetaan säännöllisesti tietoa oppimisen edistymisestä ja suoriutumisesta suhteessa asetettuihin matematiikan tavoitteisiin. Arviointi ohjaa oppilaita kehittämään matematiikan osaamistaan ja ymmärtämistään sekä pitkäjänteisen työskentelyn taitoja. Palaute auttaa oppilaita huomaamaan, mitä tietoja ja taitoja tulisi edelleen kehittää ja miten.
Oppilailla on aktiivinen rooli arvioinnissa. Itsearvioinnissa oppilaat oppivat asettamaan tavoitteita oppimiselleen ja havainnoimaan edistymistään suhteessa tavoitteisiin. Lisäksi oppilaita ohjataan kiinnittämään huomiota tapaansa työskennellä sekä tiedostamaan asennettaan matematiikan opiskelua kohtaan.
Oppilailla tulee olla mahdollisuus osoittaa osaamistaan eri tavoin. Arvioinnin kohteena ovat matemaattiset tiedot ja taidot sekä niiden soveltaminen. Lisäksi arvioinnissa kiinnitetään huomiota tekemisen tapaan ja taitoon perustella ratkaisuja sekä ratkaisujen rakenteeseen ja oikeellisuuteen. Arvioinnissa otetaan huomioon myös taito hyödyntää välineitä mukaan lukien tieto- ja viestintäteknologiaa.
Yhdessä työskenneltäessä arvioidaan sekä ryhmän jäsenten että koko ryhmän toimintaa ja tuotosta. Tuotoksen arvioinnissa kiinnitetään huomiota tuotoksen matemaattiseen sisältöön ja esitystapaan. Palautteella ohjataan oppilaita ymmärtämään jokaisen ryhmän jäsenen työskentelyn ja kehittymisen merkitys. Oppilaita ohjataan tuotosten ja toiminnan arvioimiseen.
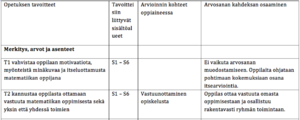
Päättöarviointi sijoittuu siihen lukuvuoteen, jona matematiikan opiskelu päättyy kaikille yhteisenä oppiaineena. Päättöarvioinnilla määritellään, miten oppilas on opiskelun päättyessä saavuttanut matematiikan oppimäärän tavoitteet. Päättöarvosana muodostetaan suhteuttamalla oppilaan osaamisen taso matematiikan valtakunnallisiin päättöarvioinnin kriteereihin. Matematiikassa oppilaan osaaminen kehittyy eri tavoitealueilla oppimäärän päättövaiheeseen saakka. Päättöarvosanan muodostamisessa otetaan huomioon kaikki valtakunnalliset päättöarvioinnin kriteerit riippumatta siitä, mille vuosiluokalle vastaava tavoite on asetettu paikallisessa opetussuunnitelmassa. Oppilas saa arvosanan kahdeksan (8), mikäli hän osoittaa keskimäärin oppiaineen kriteerien määrittämää osaamista. Arvosanan kahdeksan tason ylittäminen joidenkin tavoitteiden osalta voi kompensoida tasoa heikomman suoriutumisen joidenkin muiden tavoitteiden osalta.
TAULUKKO PÄÄTTÖARVIOINNIN KRITEEREISTÄ
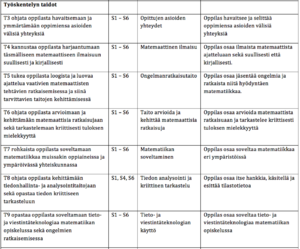
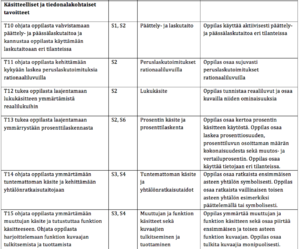
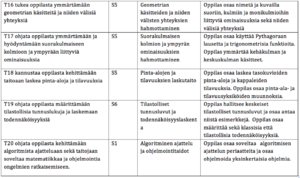
Laaja-alainen osaaminen
Ajattelu ja oppimaan oppiminen
- Oppilasta ohjataan ilmaisemaan ajatuksiaan matemaattisesti. Ohjataan ottamaan vastuu omasta oppimisestaan ja arvioimaan taitojaan realistisesti.
Kulttuurinen osaaminen, vuorovaikutus ja ilmaisu
- Ohjataan täsmälliseen matemaattiseen ilmaisuun ja perustelemaan ratkaisuaan muille.
Itsestä huolehtiminen ja arjen taidot
- Ohjataan hyödyntämään opittuja taitoja oppituntien ulkopuolella. Otetaan vastuuta omasta oppimisesta.
Monilukutaito
- Vahvistetaan kuvaajien ja matemaattisten merkintöjen lukutaitoa.
TVT-osaaminen
- Sovelletaan TVT-taitoja matematiikan opiskelussa.
Työelämätaidot ja yrittäjyys
- uskallusta käyttää tieto- ja viestintäteknologiaa
- kannustetaan täsmällisyyteen ja työvälineistä huolehtimiseen
Osallistuminen, vaikuttaminen ja kestävän tulevaisuuden rakentaminen
- Ottaa vastuuta yhdessä ja yksin matematiikan oppimisesta. Soveltaa matematiikkaa ympäröivässä yhteiskunnassa.
Vuosiluokka 7
Tavoitteet
OPETUKSEN YHTEISET VALTAKUNNALLISET TAVOITTEET T1-T20
- Opetuksen tavoitteena on vahvistaa oppilaan motivaatiota, myönteistä minäkuvaa ja itseluottamusta matematiikan oppijana. Oppilasta kannustetaan ottamaan vastuuta matematiikan oppimisesta sekä yksin että yhdessä toimien.
- Oppilas syventää matematiikan työskentelytaitoja yksin ja ryhmässä. Oppilas oppii erilaisia laskutoimituksia rationaaliluvuilla ja ratkaisemaan yhtälöitä käyttäen esim. värisauvoja, laskukiekkoja, murtokakkuja, kymmenjärjestelmävälineitä tai sopivaa sovellusta.
- Oppilas syventää osaamistaan tilastojen käsittelyssä ja tulkitsemisessa taulukkolaskentaohjelmaa apuna käyttäen.
Sisällöt
- Matematiikan työskentelytaidot
- Kokonaislukujen laskutoimitukset
- Desimaalilukujen laskutoimitukset
- Murtolukujen laskutoimitukset
- Lukujen jaollisuus
- Itseisarvo
- Vastaluku
- Käänteisluku
- Potenssin käsite
- Neliöjuuri
- Yhtälön ratkaisemisen, alkeet
- Verrannon ratkaiseminen (mittakaava, arkielämän sovellukset)
- Tarkka arvo ja likiarvo
- Pyöristäminen
- Lukujonot
- Tilastolliset tunnusluvut (keskiarvo, tyyppiarvo, frekvenssi, suhteellinen frekvenssi, mediaani, hajonta)
- Taulukkolaskenta (kuvaajien piirtäminen)
Vuosiluokka 8
Tavoitteet
OPETUKSEN YHTEISET VALTAKUNNALLISET TAVOITTEET T1-T20
- Opetuksen tavoitteena on vahvistaa oppilaan motivaatiota, myönteistä minäkuvaa ja itseluottamusta matematiikan oppijana. Oppilasta kannustetaan ottamaan vastuuta matematiikan oppimisesta sekä yksin että yhdessä toimien.
- Oppilas oppii laskemaan potenssilaskuja ja polynomien peruslaskutoimituksia käyttäen tarvittaessa välineitä esim. värisauvoja, murtokakkuja, algebralaattoja, palikoita tai mahdollisia sovelluksia.
- Oppilas syventää yhtälönratkaisutaitojaan.
- Oppilas laajentaa taitojaan tasogeometriassa käyttäen työskentelyn apuna välineitä ja rakentelua.
- Oppilas syventää taitojaan prosenttilaskennassa.
- Oppilas syventää taitojaan graafisessa ohjelmoinnissa.
Sisällöt
- Potenssilaskenta
- Polynomin käsite ja laskutoimitukset
- Yhtälöt
- Epäyhtälöt
- Vaillinainen toisen asteen yhtälö
- Tasogeometria (piste, jana, kulma, viiva, puolisuora, monikulmioiden piiri ja pinta-ala, ympyrän kehän pituus ja pinta-ala, kaaren pituus ja sektorin pinta-ala, yhdenmuotoisuus, yhtenevyys, kehä- ja keskuskulma, Thaleen lause)
- Pythagoraan lause
- Prosenttilaskenta
- Graafinen ohjelmointi
Vuosiluokka 9
Tavoitteet
OPETUKSEN YHTEISET VALTAKUNNALLISET TAVOITTEET T1-T20
- Opetuksen tavoitteena on vahvistaa oppilaan motivaatiota, myönteistä minäkuvaa ja itseluottamusta matematiikan oppijana. Oppilasta kannustetaan ottamaan vastuuta matematiikan oppimisesta sekä yksin että yhdessä toimien.
- Oppilas oppii havaitsemaan ja ymmärtämään oppimiensa asioiden välisiä yhteyksiä.
- Oppilas tutkii funktioiden ominaisuuksia ja oppii tuottamaan kuvaajia myös jonkin ohjelmiston avulla.
- Oppilas oppii ratkaisemaan yhtälöpareja.
- Geometriassa oppilas tutkii suorakulmaisen kolmion ominaisuuksia sekä kappaleita.
- Oppilas osaa laskea suorakulmaisen kolmion osia sekä kappaleiden pinta-aloja ja tilavuuksia.
- Oppilas osaa tutkia ja määrittää erilaisia todennäköisyyksiä.
- Oppilas harjoittelee yksinkertaisia todistuksia liittyen opiskeltaviin asioihin.
- Oppilas tutustuu johonkin ohjelmointikieleen ja varmentaa graafisen ohjelmointikielen hallintaa.
Sisällöt
- Funktioiden ominaisuudet ja piirtäminen
- Yhtälöparien ratkaiseminen piirtämällä ja laskemalla
- Trigonometria
- Avaruusgeometria (pallo, lieriö, kartio)
- Todennäköisyys (klassinen ja tilastollinen)
- Todistamisen perusteet
- Ohjelmointikieleen tutustuminen